Can we make a modern reproduction of the classic top octave generator / top octave synthesiser chips of the 1970s, as used in classic string synths and combo organs? What would be involved? Can we improve on the originals in any way? This page is a summary of what I learned by doing it.
A little background
In the late 1970’s, many synth manufacturers were thinking about producing polyphonic instruments. One musical area where that was already done was in the electronic organs of the time, and so the technology used in organs found its way into synths, and gave birth to the sub-genre known as “string synths”, since that was the best noise they made! Most of these instruments are fully polyphonic – e.g. you can press all the keys down and hear all the notes, although some of them use only a single envelope generator and filter for note shaping (“paraphonic”). So how did these things work?
How do string synths and organs work?
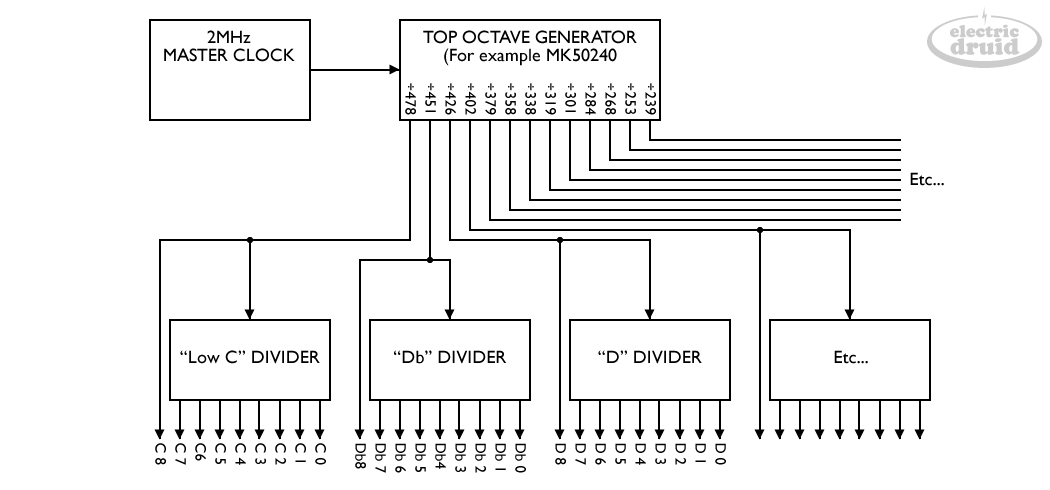
In general, they used the following scheme. A high frequency clock (typically 1 or 2MHz, sometimes 4MHz) drives a top octave generator chip (“TOG”, also known as a “Top octave synthesiser”, “TOS”, or “top octave divider”) which produces all the note frequencies for the top octave as basic square waves. These square waves can then be fed to flip-flop dividers to produce a note an octave lower. The output of that flip-flip can then be fed to another flip-flop to get an octave below than that, and so on. Luckily, we don’t need a ton of individual flip-flop chips, because that arrangement is basically a binary counter, and there are many counter chips available which will produce all the required octaves when fed the highest note frequency.
This all uses quite a few chips (one oscillator of some type, the top octave generator, and twelve dividers) but it produces all the tones you need for an entire organ – around 100 pitches. One hundred pitches from fourteen chips is pretty good, especially in the Seventies!
Can we reproduce this with modern technology?
There are easy bits and hard bits. The dividers are the easy bits, since there are still plenty of divider and counter chips available that would do the job. The difficult bit is the Top Octave Generator. This requires twelve separate dividers that can divide by large numbers (up to ÷478), and it needs to work at least the 2MHz input frequency that the originals managed. There are various ways to attempt this. One obvious solution is to use “custom hardware” in a programmable logic device like a CPLD or a FPGA. Given a large enough device with enough gates, this would work, but it’s not the easiest or most accessible solution. An alternative is to attempt to recreate the dividers in software.
So, can you program a PIC to make a TOG/TOS chip?
You can easily write code to produce a “divide by X” scheme. If we assume our instruction clock rate is the master clock, we’d simply need to output a pulse for each X instructions. We could even hard-code this for maximum speed and efficiency. It’d look something like this:
DividerLoop: bsf OUTPUT_PIN ; Set the output pin high nop ; Do nothing for many instructions until pulse goes low nop ; Etc - add the required number of "nop"s in here bcf OUTPUT_PIN ; Set the output pin low again nop ; Do nothing until pulse goes high again nop ; Etc - add the required number of "nop"s in here goto DividerLoop
This approach works fine for generating a single note, but it doesn’t scale up to multiple notes at all. The required division ratios are not simple multiples of each other (they’re approximations to numbers related by the twelfth root of two – Ouch!) and that means that there’s no simple cycle of outputs we can run through. In fact, the output sequence doesn’t repeat for a very long time. However, there’s another way.
An alternative scheme
How about if we organise the work like this instead?
Here we have no separate top octave chip. Instead, each divider produces a single note frequency and then all the octaves from it. This is much simpler to do, since now our software only has to produce one divider and the subsequent octaves. The Druid “NOTEDIV” code for this is below.
One way to think about this code is that we’re producing naive, non-bandlimited square waves at an output sample rate of 8MHz. This is a divider scheme, not an NCO/DDS with a phase accumulator, so there’s no jitter in the edges. Instead, we accept the limited frequency accuracy of the divider method.
This code uses sample-accurate delay routine. At 8MHz, that’s 125nsecs. Since we have more than 8 outputs, we can’t change them all at once (the output port registers are only 8 bits wide). This means there’s a 2 instruction/250nsec delay between the update for certain outputs. For audio frequencies, this isn’t significant.
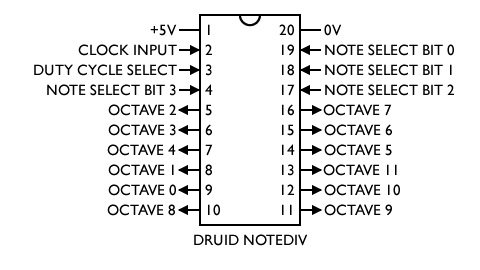
The code also uses four input pins on the PIC to select between different division ratios, and then we only need one set of code rather than twelve different firmwares. This gives us a general-purpose “Note divider” chip for building combo organs and string synths.
Are there any improvements we can make over the original chips?
Well, we can run the code faster than the original chips could manage. There are plenty of cheap PICs that will run with a 32MHz clock, giving a 8MHz instruction cycle. This is at least an octave higher than the originals, and two octaves higher than many of the common TOG chips could go.
Some Top Octave chips produced 50% duty cycle waveforms (pure square waves with only odd harmonics) and others produced 33% duty cycles (narrower pulse waves with a marked 2nd harmonic). I was able to add an input to select between two different duty cycle options; 50% and 25%. The 25% pulse wave has the strongest 2nd harmonic of all pulse waves. All of the outputs are affected by the duty cycle choice, unlike what happens if you use dividers, where the divider outputs are bound to be 50% square waves, whatever pulse width you feed in. This is done by ANDing the output with the output an octave higher. Since all the octaves are in a binary counter, this is just ANDing the counter value with a right-shifted copy.
The PIC chips can also be run from an external clock, and they’re not fussy about what frequency it is. In fact, you can run them off an LFO if you want to and…do…really…slow…computing…!! I thought the best use for this facility would be to run the chips from a single master high frequency VCO to which modulation could be applied, and I developed a PCB to allow me to test running a set of twelve NOTEDIV chips from the VCO on a 4046 phase locked loop chip. Unfortunately what I discovered is that there is enormous variation between different brands of 4046 chip, and even between different chips by the same manufacturer. It all worked, but I couldn’t get the range or tuning I wanted without tweaking nearly every resistor value in the circuit for each individual chip. That’s ok for a one-off or for experimenting with, but no use as a project for people who just want something simple to help them build the string synth of their dreams. As a result, my development of this idea got back-burnered at this point, but I do have a few PCBs and NOTEDIV chips, so if you’re interested in taking it further and would like one, contact me.
Pinout Diagram
More details
This is as far as I got with this. I do have a schematic for the PCB which I’ll put up at some point.
- Note generator PIC 16F1828 ASM code NOTEDIV
- Assembled NOTEDIV HEX code from above file
- NOTEDIV datasheet (unfinished)
- NOTEDIV schematic page 1
- NOTEDIV schematic page 2
- NOTEDIV schematic page 3
Other possibilities
If you don’t want external pitch modulation, it would possible to modify the code to use the internal clock on the PIC. This would mean that you’d have free-phase notes, although octaves would still be phase locked (this is typical for electronic organs anyway, and is a part of the sound). Using an external crystal would give the most stable and accurate results, but in some ways, that’s not the point here, and it might be that the internal RC oscillator would be good enough.
Hi,
with a cheap Altera CPLD board from China you can program 5 or 6 octaves of free phase signals, or using two obviously 10 or 12 octaves. The signals have extremely accurate frequencies as the starting frequency/clock is 48MHz, much better than 1 Cent. It’s also possible to make all signals have a 1:1 mark/space ratio (square wave).
Cheers,
Very interesting, Gordon. I’ve never played with CPLDs. That’s nice work to get all that on one chip!
How do you control the gating of the tones by the keyboard? I’ve been thinking about it since, and it seems to me like this part is in some ways a harder problem than the top octave generation – and similarly, the chips which used to provide a solution are no longer available.
Thanks,
Tom
Tom,
Exactly! The TOS/TOG is the easy part. Then comes the switching and the 9×61 (or 9×85) = 549 resistors to the nine foot registers 16′ to 1′. I have used MAX7426/7 switched capacity filters which turn a complete octave of square waves into perfect sine waves. But of course all the signals of this octave are then on one wire – so the filters have to be after the 9 registers – ie 45 filters – which wouldn’t be soooo bad. My old brain is however having trouble figuring all this out. Regards gating of the keyboard – I can easily send the keyboard signals (or through a converter board from Midi) to the CPLD EPM1270T144 to switch the outputs – but then we don’t have any attack/sustain (CPLD with analogue functions would be interesting!), so we need switching circuits after the CPLD TOG. I don’t know if a CPU could do all this? Guess it’s all ‘cos I’m stuck in the old ways – as I recently wrote in a forum -‘Now that we don’t need ’em any more, top octave sythesizers have become very easy to make’.
Very interesting. Ive been looking for a good solution for this as Ive got the ensemble and filter boards from an organ and would like the 8 octaves of strings to match. So leaving message to follow mostly, not much I can add other than Id be a willing tester.
I wonder if the divider chips could have a MIDI stack and you could have them multidrop listening to the MIDI stream and gate the outputs appropriately. Sustain would be the obvious problem, of course.
I imagine it would be a challenge handling the MIDI interrupts while updating the divider outputs.
However, I’ve seen some of your code and if anyone could do it, you could. 🙂
Interesting idea. You’re quite right that the challenge is in keeping the divider outputs updated whilst also doing the MIDI in a timely manner. The way I’ve done the dividers currently, I don’t think it would work, since I’ve had to use instruction-cycle-accurate delays to get the correct pitches and make it work. But the code *does* spend quite a while hanging about in those delay loops, so I suppose it could be processing MIDI then instead. Maybe.
I do keep thinking about this, because being able to generate the right pitches is only half the battle. The other half is gating them. I’ve been wondering about using R-2R ladder DACs to be able to output multiple mixed tones (an 8 foot pitch output, for example) since even a four bit output would be cable of handling 16 square wave tones. That’s a pretty big saving of pins.
Dunno – it’s just a thought I’m still kicking around. I don’t know yet how practical it is in software.
Tom
An interesting idea. I was looking into using PIC16F54 parts myself. Only I was going to simplify things by hard coding the divide ratio for each note. You can also output the note with:
;initialization code here.
tone_loop:
nop
nop
;etc more nops as needed.
decfsz PortB,1
decf PortA,1
goto tone_loop
oops,
needs to be:
incf PortB
btfsc Status,Z
incf PortA
goto tone_loop
how about using a cheap 8pin 12F and tweeking the internal resonator to land on the top note? Have one octave count of those parts. How stable would that be?
It’d work well enough. I can’t remember the figures for the internal RC osc, but they’re in the datasheet. It’s not bad, but it varies with temperature.
I have actually tried this. I did a set of the NOTEDIV chips set up to run off the internal oscillator – it’s a easy tweak to the config code in the firmware. Then each chip is a free-phase osc, plus the octave divider.
I am an organist and electronics tech of several decades repairing organs that use Top Octave Generator chips, one, the Conn 652 theatre uses 7 x TOG on one card a MK50241 to provide generation of solo voices and tuned percussion for the organ. There are quite a lot of these organs still about and really you need to replace a u/s chip with one that will do the same job. Why can’t we manufacture these chips again instead of relying on old chips that are becoming scarce as hen’s teeth or so expensive that you can’t afford to buy them ?
There are some clones done with FPGAs these days, as you’re probably aware, but the original chips are so expensive these days that there’s not much incentive for them to sell them cheaply. The code required to put a TOG on an FPGA is pretty basic stuff, but then there’s a PCB and getting the pin-out to match some ancient DIP IC, and it will need to be assembled (since you probably don’t want to solder an FPGA by hand) and for the small numbers we’re talking about that will be significant.
I programmed an Arduino Pro Mini (AtMEGA328P 16MHz crystal) to emulate a 12 note Top Octave Generator (e.g. MK50242) running off a 2MHz clock. Cheap solution, cost less than $3.
Hi, I’m interested in what you did. Would you send me by e-mail, all that concerns the creation of the octave generator emulator mk50240p?
Email: giovenuti@libero.it
Thank you .
I’d be interested too, is it possible to get information about it? Thank you
Hiya Tom,
One of our readers asked about how to make a TOG, and we’ve got a great solution!
https://hackaday.com/2018/05/24/ask-hackaday-diy-top-octave-generator/
https://hackaday.com/2018/08/22/ask-hackaday-answered-the-tale-of-the-top-octave-generator/
It’s more like the original circuit than your approach: one cheap import Arduino clone + 12 counters to divide all the notes down. I’ve built one into a five-octave pentatonic keyboard thing for my son, and it’s a lot of fun.
Hi Tom,
this is very interesting. I was reading your code and while I can follow most of it, some details of PIC Assembly escape me.
In particular, I could not quite get how the counter update lines work. You seem to be setting the LO to 8 and HI to 0 but
I don’t see how they get incremented. Would you mind explaining these?
; Update the count
movlw D’8′
addwf OUTPUT_LO, f
movlw D’0′
addwfc OUTPUT_HI, f
Is OUTPUT_LO etc accumulating? E.g, 8, 16, 24, 32? And if so how is OUTPUT_HI ever going to be non-zero?
Sorry about the questions, I’ve never written any PIC code before but I got really curious.
Hi Victor,
“movlw” is “move a literal value to W”, so movlw D’8′ puts 8 in the W register.
“addwf” is “add W to F” (F is used to denote memory locations). So then 8 gets added to OUTPUT_LO, as you suspected. The important bit is that the carry flag is also set if the value overflows the 8-bit value.
The next line puts zero into the W register – movlw D’0′.
Finally we have “addwfc OUTPUT_HI” which adds the W value *and the carry flag* to the memory address OUTPUT_HI. Since the W value is always zero, all we’re really doing is adding the carry on when required.
This is how multi-byte addition is done on these chips.
Thanks, the F placeholder was what confused me. I get it now.
Great job.
A while ago I did a MIDI-to-61-key divider based on a XC6SLX9 FPGA ($6-$17 depending on where you source it from), with pitch-bend and LFO. The uncool part was doing the per-key filtering, and trying to make the keys sound similar. The cool part, you only need a few components and presto (fpga, spi mem, clock gen, midi optocoupler circuit).
However, be careful. If you check the *king* of the divide-down specimes, the ARP Solina, it uses a SAA1030 as top divider. The (german) datasheet reports that the clock has to be adjusted to 4,688.64 MHz.
That is to produce the top octave, with A5 in that octave being 7,040 Hz (16 x 440 Hz).
Then, 4,688,640 / 7,040 = 666
Finding that was the signal for me to do something else 😀
Dear,
I have a 1975 Hammond X-5. Someone used the opportunity and took out a block, a Tone Divider board, and the Tone Mixer board too. Hammond is old but of an extraordinary tone and I would like to complete it and put it back into function. I would ask you to tell me if someone have these boards, and what is the price. My I fix the problems with Flat Keys FK50240 Top Octave Synthesiser Chip PT2, bit without the missing boards. Thanks guys in advance.
Best regards.
Brana
Sorry, I don’t know of anywhere, but if anyone who sees this who could help would like to get in touch, I’ll put you in contact.
Dear Brana. I have more than 5 Hammond X-5, and I have made the substitute board with the MK50240, if You are interested. You can mail me directly at soeren-poulsen@hotmail.com
Hi Tom,
I am very intrigued by the TOG divide-down scheme, particularly for making string machines. Since hardware is not my thing, I was trying to emulate this in a programming environment. Now I can’t get my head round the divide-down scheme without requiring oversampling (possibly massively), so I implemented an inverse approach:
generate low frequency phase signals and then scale them up to use with bandlimited sawtooth table lookup.
This works alright and produces the phase synchronous octaves etc, but I still wanted to see if there were any ideas on how to do a true top octave generator digitally without oversampling.
Anyway, I thought I’d add a comment here just in case I am missing something very obvious.
Thanks
The original divide-down systems ran with a master clock of (typically) 4MHz or so, so that was the effective “sample rate” for the output. That’s difficult to achieve outside hardware (dedicated processors like I demonstrated above can get close, or FPGAs can easily manage it).
I would think that the best DSP approach would be to generate a basic ramp (which can easily be scaled up/down to octaves) and then apply BLEP corrections to avoid aliasing in the final output signal:
http://metafunction.co.uk/all-about-digital-oscillators-part-2-blits-bleps/
An alternative approach would be what’s known as “mip-mapped” (from image processing) where you use a series of band-limited tables, according to what octave you’re in. This is the “DWGS” sc heme from Korg’s DW series synths from years ago:
https://electricdruid.net/wavetable-oscillators/
HTH,
Tom
Hi Tom,
yes, the wavetable approach is what I use (I prefer it to blep etc), but as said it is an upside-down way, produce the phase ramps in the lower octave and scaled them up to the higher octaves, then look up the corresponding table.
I think dedicated HW is needed alright for a TOG and FPGAs seem an obvious choice. I don’t have any experience with these, so I have some open questions in my head (e.g. do we run the synthesis fully at a MHz sampling rate? At what moment do we decimate and produce a signal
at a normal rate? or do we use a DAC at the end, converting at that high rate?)
I have seen that commercial synthesisers are now using FPGA oscillators and analogue filters, and I had the same question about the SR and the DAC, whether it all runs at a such a high SR, nearly approximating a continuous signal, and the conversion is done at that high rate.
Maybe that’s what I need to do next, play around with an FPGA board.
Thanks
I think you’ll find that most of those approaches have been tried in one instrument or another. I’m pretty sure some of the Waldorf stuff that uses dedicated hardware down-samples fairly early and outputs via a DAC at a normal rate. But the recent Novation Peak does it the other way and uses a many-MHz sample rate right until the output. Details in both cases are proprietary, unfortunately!
Whilst all this micro controller experimentation is very interesting
It all depends on what you are actually trying to do.
If its building a 1 off Organ or String Synthesizer project Then there are plenty of Free to collector Organs where you can salvage parts rather than reinventing the wheel.
Before you had TOG/TOS Chips top octave generators were done with 12 tuned coil circuits This was how the Yamaha B10BK was done.
Organs like the Vox Continental used a Method similar to Tom’s approach where a single top octave tone was divided on a single board (rather than a chip) and then 12 differently tuned boards fitted to give all the tones required.
If however you are trying to fix a vintage organ/synth that uses a TOG/TOS chip then you have a few options try to salvage the parts from another less valuable organ, make a single oscillator to replace the missing tones from you TOS if that’s the issue or buy a cloned Tos from someone like Flatkeys unless you enjoy playing with code instead of making music!
I understand the divider concept well. I have many years of organ playing, best sound is discrete oscillators the out of phase sound will no be replaced with inline divider chips. Synchronized sound.
They’re different things. There’s a certain “combo organ” sound from a particular era that comes from the use of these dividers, in much the same way that the “Hammond sound” comes from its use of a tonewheel generator – that also has locked frequencies, and not at the frequencies you’d necessarily expect, and no-one complains about Hammond B-3s! Clearly neither of those have the same free phase characteristics as an actual pipe organ, but that’s a different thing again.
Free. Phase is richer with any type organ, just more expensive
@Wayne: long time ago I had a Yamaha CP-30 stage piano. It contained the full electronic for 2 pianos, both with their own TOG. Both could be tuned smoothly from -1 to +1 tone. So it was possible to tune them a very little bit differently, and – WOW! – suddenly you got a very natural sound.
Later I adapted this idea to a self-built device (see my other post). I made the difference 1/128, that means, one TOG was fed with 1,000,000 Hz and the other one was fed with 992,187.5 Hz. Same WOW effect.
Very interesting, Paul, thanks! Some of the 1970’s string synths also used two sets of master oscillator, TOG, and dividers like you describe. It’s a great way to fatten up the sound.
That’s the case with the Yamaha SS30, a contemporary of the CP30 piano. As well as dual TOG’s there is a a BBD ensemble effect for maximum wobble!
*sigh* Look at my device (see linked website) I built back when you could still buy TOGs. It constantly invents new melodies. Sorry, the website is in German, but there are photos and audio samples.
You have really good ideas on how to replace a TOG, but they would never fit in this device. My device is unique and will probably always remain so.