Practical LFSR random number generators

The linear feedback shift register is one of the most useful techniques for generating psuedo-random numbers. I’ve used this method for creating noise generators and as an element in the random modulation generators I spent a long time developing for my Protowave synth.

If you’re not really clear how an LFSR works, have a look at one of the many pages online (links below). This page isn’t here for that. In short, an LFSR takes a series of bits from a long shift register, XORs them together to come up with a resultant bit, shifts the register along one bit, and then sticks the new bit back into the beginning of the register. If the positions of the bits (the “taps”) are chosen carefully, this produces a maximal-length string of bits which is as damn near random as makes no odds to anyone other than mathematicians and cryptographers. For synth and audio use, it is easily good enough. A 32-bit LFSR will produce a sequence of over 4 billion random bits, or 500 million random bytes. If you output them as audio at 96KHz, the noise won’t repeat for an hour and a half. I think you’ll have forgotten what the beginning sounded like by then!

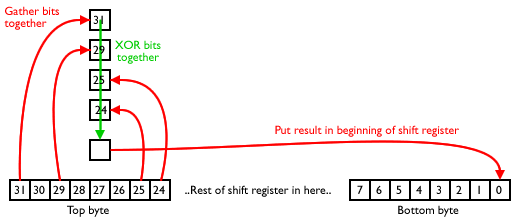
As an example, let’s take a 32-bit LFSR with four taps at positions 32, 30, 26, and 25. For some reason, LFSR taps are numbered starting on one, so take one off the tap position to get the bit that represents. So we need bits 31, 29, 25, and 24. It looks like this:

Here’s some PIC ASM code for our example LFSR:

; LFSR NOISE SOURCE
; Uses 5 bytes of memory:
; SHIFT_REG3, SHIFT_REG2, SHIFT_REG1, SHIFT_REG0, a 32-bit LFSR
; NOISETEMP is temporary storage during the calculation.
;
NoiseSource:
	;Get bits 31, 29, 25, and 24 for the feedback XOR
	; Put Bit 31 into NOISETEMP
	bsf	NOISETEMP, 0	; Assume it's set
	btfss	SHIFT_REG3, 7
	bcf	NOISETEMP, 0	; Clear it if not	

	; Invert the NOISETEMP bit if Bit 29 is set
	btfsc	SHIFT_REG3, 5
	comf	NOISETEMP, f

	; Invert the NOISETEMP bit if Bit 25 is set
	btfsc	SHIFT_REG3, 1
	comf	NOISETEMP, f

	; Invert the NOISETEMP bit if Bit 24 is set
	btfsc	SHIFT_REG3, 0
	comf	NOISETEMP, f

	; Feedback is inverted wrt the XOR output
	bsf	CARRY		; Assume it's set
	btfsc	NOISETEMP, 0
	bcf	CARRY		; Clear it if not

	rlf	SHIFT_REG0, f		; 32 bit shift
	rlf	SHIFT_REG1, f
	rlf	SHIFT_REG2, f
	rlf	SHIFT_REG3, f
	; A new random bit can be read from SHIFT_REG3,7
	; (or pretty much anywhere)
	return

This code is 16 instructions, if you ignore the return, and a similar number of instruction cycles.

The problem with the typical LFSR is that it only produces one new random bit each time you shift it. This is ok for some things (like my white noise source, but often you need a random 8-bit value (or on a dsPIC, a random 16-bit value). The obvious way to do this is to run the above code 8 times, which is ok, and works fine, but is very inefficient, since it’d need around 8×16=128 instruction cycles.

Instead, I started thinking about what happens when you run the code eight times, to see if I couldn’t get some gains from doing 8 stages of XORing and shifting at once. I’d been reading about Scott Dattalo’s vertical counters (Unfortunately Scott’s excellent website is no more) and this seemed like a logical thought.

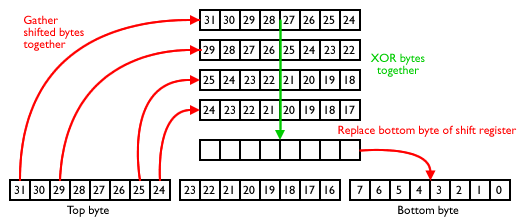
To begin with, let’s just focus on tap 32. The first time we run the code, we pull out bit 31. The next time we run it, the register has shifted, so we pull out what was bit 30. The time after that, we get bit 29, etc etc. Over the eight runs, we get all of the bits of the top byte of the register.

A similar thing happens with each of the other taps. Tap 30 gives us a byte from bit 29 to bit 22, tap 26 a byte from bit 25 to bit 18, tap 25 from bit 24 to bit 17.

I realised that the more efficient way to perform the 8 sets of XORs is to take these four bytes and XOR them together as bytes rather than bit by bit. In order to do this, I have to shift the bytes in the register so that they all line up. We can then XOR, and finish up with a result byte which has all eight of the required bits for the front of the register in it. The final step is to shift the register over 8 bits. Since this is a one byte shift, we can use movf operations rather than eights sets of bitshifts with rlf. Again, this is much quicker.

Code for this looks something like this:

; LFSR NOISE SOURCE
; Uses 11 bytes of memory:
; SHIFT_REG3, SHIFT_REG2, SHIFT_REG1, SHIFT_REG0
; NEW_REG0	The replacement SHIFT_REG0 byte
; TEMP_REG3A	Exactly what they say on the tin.
; TEMP_REG3B
; TEMP_REG2A	Temporary copies of REGs 2 & 3
; TEMP_REG2B

NoiseSource:
	; First I need to copy two bytes I'm going to muck with
	movf	SHIFT_REG3, w
	movwf	TEMP_REG3A	; I need 2 copies for left/right shifts
	movwf	TEMP_REG3B
	movwf	NEW_REG0	; Get bit 32 while we've got it
	movf	SHIFT_REG2, w
	movwf	TEMP_REG2A	; Two copies of this too
	movwf	TEMP_REG2B

	; Next, I need to XOR all the bytes together
	rlf	TEMP_REG2A, f	; Left shift 1st set of copies
	rlf	TEMP_REG3A, f
	rlf	TEMP_REG2A, f
	rlf	TEMP_REG3A, w
	xorwf	NEW_REG0, f	; XOR with bit 30
	rrf	TEMP_REG3B, f	; Right shift 2nd set of copies
	rrf	TEMP_REG2B, f
	movf	TEMP_REG2B, w
	xorwf	NEW_REG0, f	; XOR with bit 25
	rrf	TEMP_REG3B, f
	rrf	TEMP_REG2B, w
	xorwf	NEW_REG0, f	; XOR with bit 26

	; Perform a byte shift on the whole 32-bit register
	movf SHIFT_REG2, w	; Put SR2 into SR3
	movwf SHIFT_REG3
	movf SHIFT_REG1, w	; Put SR1 into SR2
	movwf SHIFT_REG2
	movf SHIFT_REG0, w	; Put SR0 into SR1
	movwf SHIFT_REG1
	movf NEW_REG0, w		; Put NEW_REG0 into SR0
	movwf SHIFT_REG0
	return

This is 27 instructions, ignoring the return, but does 8 times as much as the code above for only 10 instructions more. Certainly 27 is a lot better than 128.

Limitations and Possibilities

The only limitation is that you can’t use taps that are within the part that you replace in the final step. This is why I chose the set of taps 32, 30, 26, 25 and not the equally good 32, 30, 7, 4. Think what happens to those two low taps if we run the single-bit-shift version eight times – they get modified by new bits going into the register. My algorithm assumes this will not occur, so it only works with sets of taps where this assumption holds true.

This code is based on an arrangement known as the Fibonacci LFSR. There is an alternative arrangement called the Galois LFSR. This may offer a way to produce even more efficient code. I haven’t tried it.

Links

There seem to be lots of ways of looking at this, depending whether you’re coming at it from a hardware, software, or maths angle. It’s all the same really.

Wikipedia LFSR page – Wikipedia has a pretty good article on LFSRs, with details of the differences between the Fibonacci and Galois versions.

Xilinx – Useful application note with lists of maximal length XNOR tap sequences for registers from 3 to 168 bits in length.

EETimes, Tutorial on LFSRs – Another way of explaining the same thing. You might find this way is the way that makes the light come on for you.